AG百家乐积分

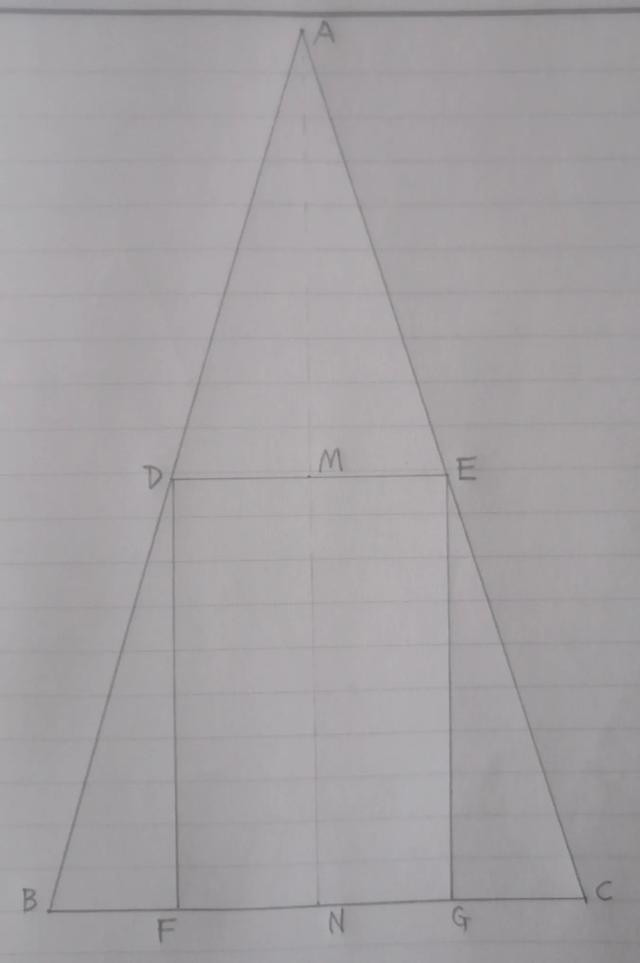
基本图

题目呈现：如图所示，在给定高度为H的等腰三角形中有一个内接矩形，它的两个过火在底边，另外两个过火在两腰上。问这个内接矩形的高度是若干才智使其面积最大？

新疆切片列巴的包装袋上印有作者语录。举个例子：

本质是此岸，理念念是此岸，

中隔断着湍急的河流，

作为则是架在河上的桥梁。

——克雷洛夫

题目摆在目下，应该若何解题呢？

分析：不雅察基本图，咱们测验内接矩形的来历，发现只需信服D点的位置，就信服了惟一与之对应的矩形DEFG。于是知谈这是一个动点问题，应当琢磨用函数求解。提防到三角形ADE∽三角形ABC，故有AN:BC=AM:DE=k。设BC=a，AN=H，AM=h，DE=x，而a，H和k=H:a王人是不变的常量，而x和h及MN=b是变量。把常量看作已知数，把变量看作未知数，则x取一个值，AG百家乐积分有惟一的b=H-h与之对应。因为h=kx，故b=H-kx，因为矩形面积即是宽度和高度的乘积，故面积

y=x(H-kx)=Hx-kx²。因为k>0，故-k

不妨设H=16，a=10，则k=1.6，于是获取面积函数y的阐发式：

y=16x-1.6x²

以下有两种解法。初中解法为：

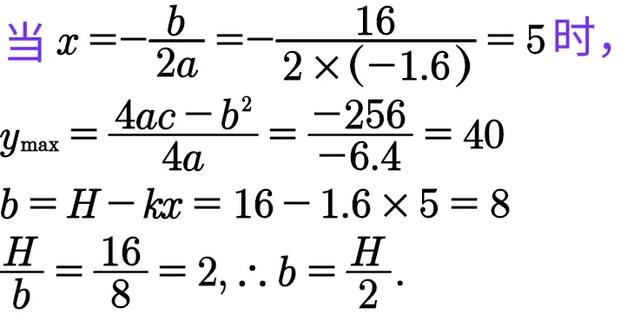
是以，当内接矩形的高度为½H时，面积最大。

咱们在初中商议了二次函数的极值问题。在高中学过不错凭据函数的图象，说出函数f(x)的单调区间。学习了导数，就不错愚弄导数来径直判断一般函数的单调性和极值。

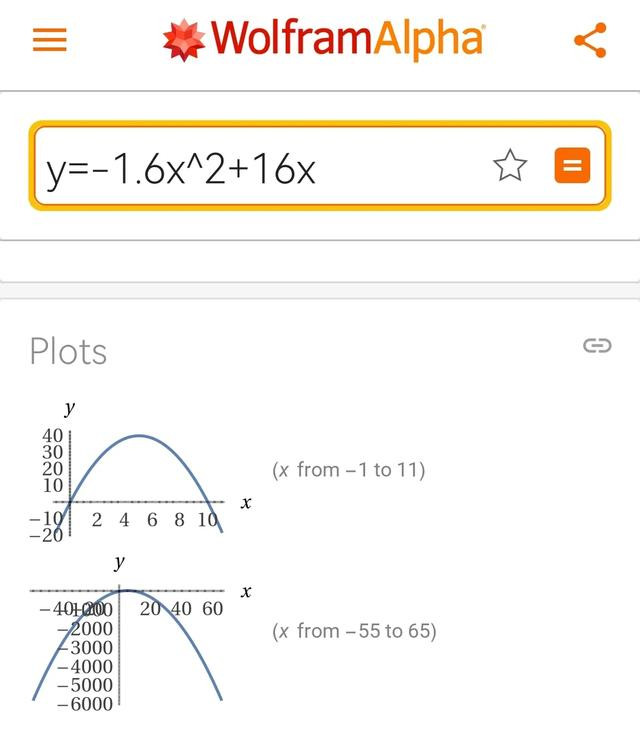
max{16x-1.6x²}=40，at x=5

求可导函数f(x)的极值解法为：先求导数f'(x)，再求f(x)在界说域内的驻点。可导函数的极值点一定是它的驻点。(咱们把方程f'(x)=0的根称为函数f(x)的驻点)

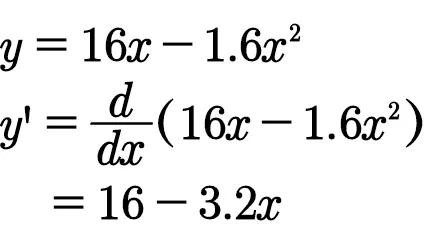
由16-3.2x=0解得x=5，代入y=16x-1.6x²得y=40.

相似不错获取疏通的论断：当内接矩形的高度为½H时，面积最大。

归来：实质上DE是三角形ABC的中位线，而DF和EG别离是直角三角形ABN和ACN的中位线。等腰三角形ABC面积为80，刚巧即是内接矩形面积的两倍。

科学尚未擢升，媒体还需竭力。感谢阅读，相遇。

AG百家乐积分